無量綱量具有數值的特性,可通過兩個量綱相同的物理量相除得到,也可由幾個量綱不同的物理量通過乘除組合得到。在科研中,無量綱數對于理論求解,實驗研究和數值計算都有指導意義。以下為流體力學中常見的無量綱數:
1 雷諾數(Re)
自然界的流體流動有兩種流態:低速流動,流體為有規則有秩序的流動,稱為層流;當流速增大時,流體逐漸轉為一種雜亂無章的流動狀態,稱為湍流。雷諾數反應了慣性力和粘性力的比值,是判斷流場處于湍流還是層流的一個數值,其表達式:
其中,ρ為密度,v為流體平均流速,d為特征長度,一般依據具體的研究問題進行選擇,μ是動力粘度。雷諾數較小時,粘滯力對流場的影響大于慣性,流場中流速的擾動會因粘滯力而衰減,流體流動穩定,為層流;反之,若雷諾數較大時,慣性對流場的影響大于粘滯力,流體流動較不穩定,流速的微小變化容易發展、增強,形成紊亂、不規則的紊流流場。
2 努塞爾數(Nu)
努塞爾數以德國物理學家 Wilhelm Nusselt 的名字命名,以紀念其該方向研究的突破貢獻。在流體邊界(表面)的熱傳遞中,努塞爾數 (Nu) 是跨越邊界的對流熱量與傳導熱量的比率。在傳熱實驗及流體仿真計算中,Nu 數是反映對流換熱能力的一個重要無量綱數。
其中,h為流體的對流傳熱系數,L 為傳熱面的幾何特征長度,λ為流體的導熱系數。
3 普朗特數(Pr)
普朗特數是表示流體中能量和動量遷移過程相互影響的無因次組合數,表明溫度邊界層和流動邊界層的關系,反映流體物理性質對對流傳熱過程的影響,其表達式:
其中,υ為運動粘度,α為熱擴散系數,μ為動力粘度,Cp為定壓比熱,λ為導熱系數。從熱物性的角度看,如果已知動力粘度、導熱系數以及定壓比熱中的任何2個參數,就可以通過普朗特數得到第3個。
4 馬赫數(Ma)
馬赫數是流體力學中表征流體可壓縮程度的一個重要的無量綱參數,記為Ma,定義為流場中某點的速度v同該點的當地聲速c之比,它是以奧地利科學家E.馬赫的姓氏命名的。
由定義可知,馬赫數是表示聲速倍數的數,一馬赫即一倍音速:馬赫數小于1者為亞音速,近乎等于1為跨聲速,大于1為超聲速。
5 畢渥數(Bi)
表征固體內部單位導熱面積上的導熱熱阻與單位面積上的換熱熱阻(即外部熱阻)之比,其表達式:
其中,δ是特征長度,h 是表面傳熱系數,λ是導熱系數。其物理意義是,畢渥數的大小反映了物體在非穩態導熱條件下,物體內溫度場的分布規律,或者認為是固體內部導熱熱阻與界面上換熱熱阻之比。
努塞爾數表達式看起來與畢渥數相同,但二者意義有本質區別,Nu數表示壁面上流體無量綱溫度梯度(λ為流體導熱系數),用于研究對流傳熱問題;而畢渥數用于研究導熱問題,為固體內部導熱熱阻與界面上換熱熱阻之比。
6 傅里葉數(Fo)
傅里葉數可以表示非穩態傳熱速率與熱存儲速率的比值,以約瑟夫·傅立葉的名字命名。
傅里葉數=(熱擴散率*時間)/厚度的二次方,物理意義是兩個時間比值的無量綱量,分子理解為物體表面發生一個有限大小的熱擾動時刻至開始計算時刻時間長度,分母可以理解為同樣的熱擾動。從發生時刻起,至其影響深度至分母中厚度時刻為止的時間長度。對兩個同心圓柱體間的定常層流進行模擬。內部圓筒以恒定的角速度旋轉引起流動,外部圓筒保持靜止。流動是穩態的。利用層流的解析方程可以計算出不同截面的切向速度。這些數值可用于與仿真結果進行比較。


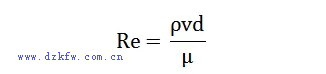
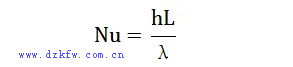
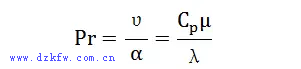
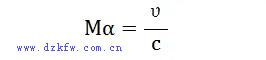
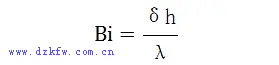
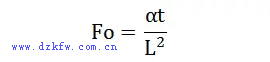
 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底